1. Introduction - Antiderivatives
2. Trig Powers
3. Trig Substitution
4. Partial Fractions
5. Other Related Topics
When you wish to integrate functions that are not in the basic list and a simple substitution will not work there are some algebraic methods that might work. This is intended to get you started and to point you in the direction of a solution method. If one of these methods does not work in a specific case, they will hopefully help you find something that will. To paraphrase Dennis Zill: Try something, you could get lucky.
At times it becomes desirable to calculate the antiderivative of
such functions as![]()
![]() and
and ![]()
![]() This section looks at problems
of this type, especially those where
This section looks at problems
of this type, especially those where ![]()
![]() and
and ![]()
![]() are non-negative integers.
are non-negative integers.
We will first look at: ![]()
![]() To integrate this type of
function you will normally use the trig identities
To integrate this type of
function you will normally use the trig identities

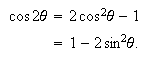
If either ![]()
![]() or
or ![]()
![]() is an odd positive integer (say m), write
is an odd positive integer (say m), write ![]()
![]() noting that since
noting that since ![]()
![]() is an odd integer
is an odd integer ![]()
![]() is an even integer. Thus
is an even integer. Thus ![]()
![]() Now use identity (a)
to make the substitution
Now use identity (a)
to make the substitution ![]()
![]() This should lead to the following:
This should lead to the following: ![]()
![]() where
where ![]()
![]() is a polynomial type function
if
is a polynomial type function
if ![]()
![]() is considered a
variable. Thus the substitution:
is considered a
variable. Thus the substitution:

If ![]()
![]() is odd, a similar substitution of
is odd, a similar substitution of
![]()
![]() yields
yields ![]()
![]() Now, using the substitution:
Now, using the substitution:

![]()
![]()

If both ![]()
![]() and
and ![]()
![]() are even, then by using
are even, then by using ![]()
![]() and
and ![]()
![]() we can change
we can change ![]()
![]() into a function of
into a function of ![]()
![]() .
.

Now to look at ![]()
![]() it is first necessary to note
that since
it is first necessary to note
that since ![]()
![]() we have:
we have:

If ![]()
![]() is a positive even integer then
the substitution
is a positive even integer then
the substitution ![]()
![]() can be used to change
can be used to change ![]()
![]() into a function of
into a function of ![]()
![]() specifically:
specifically:

The substitution:
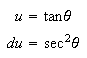
can then be used to solve the integral.

If ![]()
![]() is odd, try changing
is odd, try changing ![]()
![]() into
into

and use the substitution


If ![]()
![]() is even and
is even and ![]()
![]() odd then you must use integration
by parts.
odd then you must use integration
by parts.
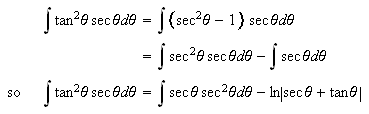

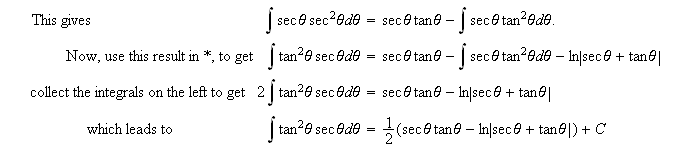
Cotangent and cosecant are approached in a similar manor to tangent and secant. In some cases negative and fractional powers can be handled very much like the above and in others observing the above methods and a little imagination can lead to desired results. Trig identities allow for some very creative work just remember to not mix functions of different angles in the same term. If they occur in different combinations than covered here (sin mixed with tan, for example), it is often useful to convert everything into sin and cos.
When integrating

we may find it necessary to allow ![]()
![]() or
or ![]()
![]() and use the Pythagorean
identities to simplify the function combination
and use the Pythagorean
identities to simplify the function combination ![]()
![]() into a function of trig powers
as talked about in the previous section.
into a function of trig powers
as talked about in the previous section.
First look at ![]()
![]() :
:


which, in some cases, may be easier to handle.

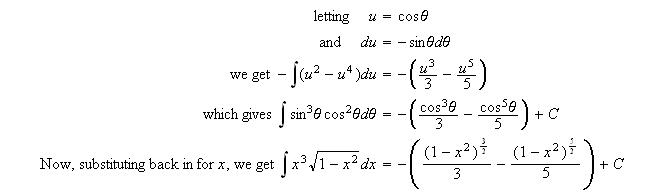
Likewise, since ![]()
![]() , when the substitution
, when the substitution
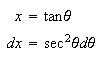
is applied to ![]()
![]() we get
we get ![]()
![]()
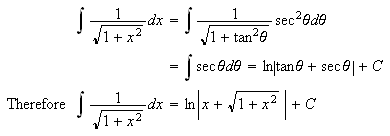
Also, since ![]()
![]() the substitution
the substitution
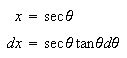
will give ![]()
![]()

We can generalize these in the following manner, for ![]()
![]() , we can
substitute
, we can
substitute ![]()
![]() to get
to get ![]()
![]() . A similar substitution can be
used in the other cases.
. A similar substitution can be
used in the other cases.
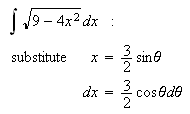
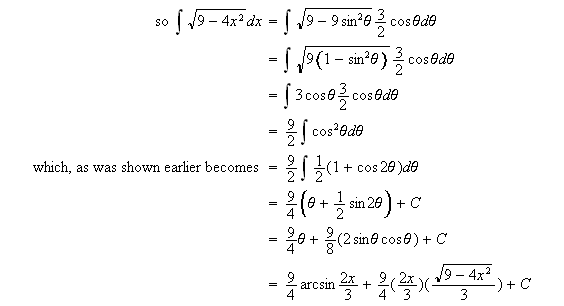
If ![]()
![]() and
and ![]()
![]() are polynomials
in
are polynomials
in ![]()
![]() then
then ![]()
![]() is called a rational algebraic
expression (RAE), i.e. an algebraic fraction. To find
is called a rational algebraic
expression (RAE), i.e. an algebraic fraction. To find![]()
![]() first be sure that the degree of
first be sure that the degree of ![]()
![]() is less than the
degree of
is less than the
degree of ![]()
![]() this makes
this makes ![]()
![]() a ''proper'' rational algebraic
expression (PRAE). If this condition does not exist then it becomes
necessary to use division to achieve this condition.
a ''proper'' rational algebraic
expression (PRAE). If this condition does not exist then it becomes
necessary to use division to achieve this condition.

To finish this problem one must integrate![]()
![]() a PRAE.
a PRAE.
Theoretically, at least, every polynomial in ![]()
![]() can be factored into a set of
linear and quadratic factors with real coefficients. Realistically, it
is not always reasonable to do this; however, when you can factor the
denominator into this type of set then the method of breaking the RAE
into its partial fractions gives an algebraic breakdown into simpler
fractions that may be integrated by other methods such as: (ignoring
the constants of integration)
can be factored into a set of
linear and quadratic factors with real coefficients. Realistically, it
is not always reasonable to do this; however, when you can factor the
denominator into this type of set then the method of breaking the RAE
into its partial fractions gives an algebraic breakdown into simpler
fractions that may be integrated by other methods such as: (ignoring
the constants of integration)

for example. (These are the more common examples.)
To understand partial fractions one must remember certain basic algebra concepts. They are:
There exists ![]()
![]() and
and ![]()
![]() such that
such that ![]()
![]()
When ![]()
![]() is a polynomial in
is a polynomial in ![]()
![]() of degree
of degree ![]()
![]() than
than ![]()
![]() and
and ![]()
![]() are all polynomials in
are all polynomials in ![]()
![]() of degrees less that
of degrees less that ![]()
![]()
If ![]()
![]() is a PARE then,
when
is a PARE then,
when ![]()
![]() and
and ![]()
![]() are polynomials,
are polynomials, ![]()
![]() and
and ![]()
![]() will all be polynomials of
degrees less than the degrees of
will all be polynomials of
degrees less than the degrees of ![]()
![]() and
and ![]()
![]() , respectively. Thus, if
, respectively. Thus, if ![]()
![]() is a PARE then
is a PARE then ![]()
![]() and
and ![]()
![]() are also PARE's.
Hence if
are also PARE's.
Hence if ![]()
![]() (linear) then
(linear) then ![]()
![]() a constant and if
a constant and if ![]()
![]() (quadratic) then
(quadratic) then
![]()
![]() a linear binomial, etc..
a linear binomial, etc..
If ![]()
![]() then
then ![]()
![]() for every
for every ![]()
![]()





Now to finish the opening example (Again equating coefficients to
complete the partial fractions and disregarding the constant of
integration for the moment):
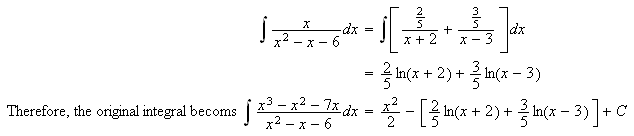
In the case of repeated linear factor(s) of the denominator, the partial breakdown will look like this:

Notice that the partial breakdown includes a fraction with a
constant numerator (![]()
![]() are constants)
for each power of the repeated factor from 1 to n. This is possible
since the common denominator is
are constants)
for each power of the repeated factor from 1 to n. This is possible
since the common denominator is ![]()
![]() giving:
giving:

With repeated quadratic factors we get fractions with linear numerators:

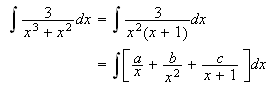
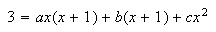

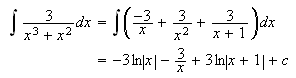
To integrate functions involving ![]()
![]() or
or ![]()
![]() ,
,![]()
![]() you may find it advantageous to
complete the square. Remembering your algebra you will get
you may find it advantageous to
complete the square. Remembering your algebra you will get



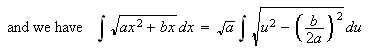
which can be solved using trig substitution. Likewise the same
approach leads to

which can be solved by using partial fractions since ![]()
![]() .
.
Completing the square is also useful on forms such as ![]()
![]() and
and ![]()
![]() where
where ![]()
![]() is a
non-factorable quadratic.
is a
non-factorable quadratic.
In order to find the antiderivative of

try combinations (![]()
![]() of the following trig identities
to get an integral of terms of sine or cosine only.
of the following trig identities
to get an integral of terms of sine or cosine only.
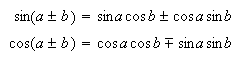

Now a word about the definite integral. Recall that it is the algebraic sum of the areas between the curve, the dependant axis, and the end lines. Thus it can be found using known area formulas or estimated using the Riemann sum. We also know that if the function has a known antiderivative the exact answer can be found by using the Fundamental Theorem of Calculus. Sometimes, the calculations by these methods may be difficult and we latch onto any tool that might shorten and/or simplify the work. One of the nice shortcuts occurs when the function to be integrated is either even or odd.
Remember that a function is even when ![]()
![]() and is odd when
and is odd when ![]()
![]() . It should be noted that not all
functions fall in one of these two categories. A look at the graph of
these functions leads to a very easily verified observation:
. It should be noted that not all
functions fall in one of these two categories. A look at the graph of
these functions leads to a very easily verified observation:
If ![]()
![]() is even then
is even then ![]()
![]() and
and
If ![]()
![]() is odd then
is odd then ![]()
![]()
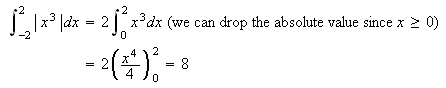
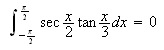
I will close this discussion of methods of integration with one
last example. This example requires a little imagination and creative
use of several methods. (i.e. it is fun!) Integrals similar to this
appear often in Physics.
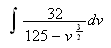
Letting
![]()
![]() and
and ![]()
![]() we get:
we get:

Equating coefficients (also known as using undetermined coefficients) we have:
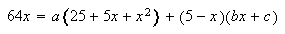

Thus, after completing the square on the denominator of the second
fraction and adjusting the numerator we get:
