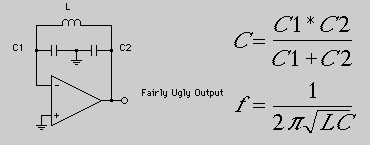
Colpitts Oscillator
The Colpitts oscillator is a phase shift oscillator using inductors and tapped capacitors. Using an op amp, the Colpitts oscillator circuit is given below. The tapped capacitor is a capacitor where C1 and C2 share the same dielectric. The electric field being shared means that the voltages across C1 and C2 are equal.
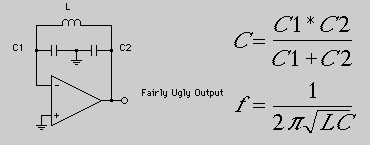
While intended to be built using tapped capacitors, the above circuit also works well enough with discrete capacitors. For a signal at the resonant frequency of the LC combination, the impedance around the LC loop is simple the resistance of the coil. Substantial currents and voltages can result, with the op amp making up the ohmic losses in the system.
Hartley oscillators are the reactive complement for the Colpitts oscillator. Instead of a tapped capacitor, a tapped inductor (transformer) is used.
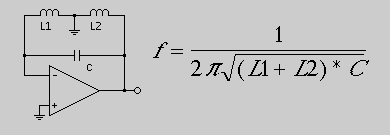
The Armstrong oscillator uses a transformer and capacitor to achieve the phase shift necessary for oscillation.
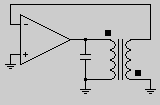
Saturation governed oscillators are non-linear switching devices that use positive feedback to keep a transistor turned on while collector current builds. As soon as the transformer saturates, base current disappears, causing the transistor to cut-off, diverting the current to a load, in this case, a neon bulb. The period of oscillation is given by the volt-sec rating of the transformer core, coupled with operating voltage.
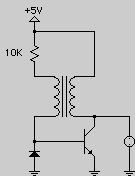
Build the Colpitts oscillator using C=0.01uF and L being any convienent value. (33 uH works fine.) If you use discrete capacitors, as opposed to center tapped capacitors, remove C2, and explain your circuit's behavior.
Find a small signal transformer and build the Hartley, Armstrong and saturation oscillators.