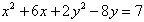
Each problem on this sheet represents a type of problem you will
need to remember how to do at some point during the three-semester
calculus sequence. Take this home and work on it, with whatever
help you need and can get. If you cannot do almost all of these
problems confidently, with help, then you should consider taking
a prerequisite course to review the material. All of these topics
are on the syllabus of MTH 1764, Precalculus, which is the prerequisite
for MTH 1854, Calculus I. In some cases, these are review topics
and were covered in MTH 1753, Trigonometry.
Many students need an extra review of trigonometry. A list of
trigonometry facts
is available on the Web and a few additional trigonometry problems,
with discussion and solutions, are available on the Web.
1. Describe the graph of this equation in words
and then sketch it: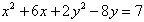
2. Describe the graph of this equation in polar coordinates and
sketch it.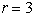 
3. Sketch graphs of these two functions and describe their domains
and ranges, asymptotes and intercepts: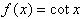 
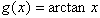
and 
4. Sketch graphs of these two functions, describing in words how
they are related to each other. Find all asymptotes and intercepts
of each.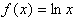 
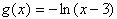
and 
5. For the line through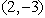 
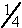
with slope 
,
find the equation in slope-intercept form.
6. Prove this trigonometric identity: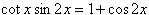 
7. Find all solutions in 
: 
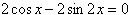
In 8-12, solve for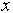 
. Find all real and
complex solutions.
8. 
9. 
10. 
11. 
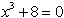
12. 
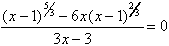
13. Solve this system of equations: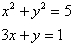 
14. Find all points of intersection that have real coordinates:
and 
.
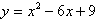
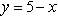
15. The half-life of a certain radioactive substance is 1200 years.
If 5 grams of it is spilled, how long will it be before only 1
gram is left?
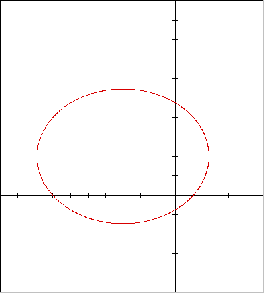
1. Recognize this as an analytic geometry problem - circle or
ellipse since both x and y are squared, ellipse because the coefficient
of the squared terms are different. Use completing the square
separately on the x parts and the y parts to write it in the form
that makes it easy to read the center from the equation.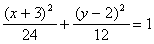 
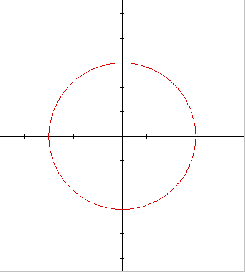
So the center is at (-3, 2).
2. Recognize this as a circle with center at the origin and radius
3. (see above right)
3. The cotangent function has domain all numbers except integer
multiples of pi (and the integer multiples of pi are vertical
asymptotes) and range all real numbers. It has no horizontal asymptotes.
The arctangent function has domain all real numbers and range
all numbers between negative pi/2 and positive pi/2. It has no
vertical asymptotes and horizontal asymptotes at negative pi/2
and positive pi/2.
Cotangent function Arctangent function
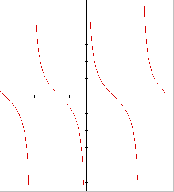
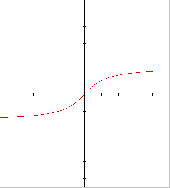
4. The minus three shifts the graph three units to the right horizontally.
The minus in front reflects it across the x axis. Neither function
has a y intercept nor a horizontal asymptote. The x intercepts
are (1,0) for the first function and (4,0) for the second function.
The vertical asymptote is x=0 for the first function and x=3 for
the second function.
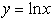
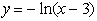
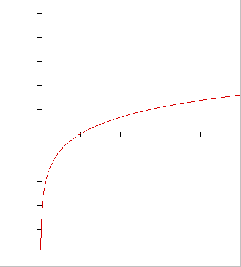
5. Use the point-slope form of a line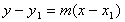 
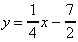
and then, after plugging in the point and the slope, solve for
y to put it in slope-intercept form. The solution is 
.
6. 
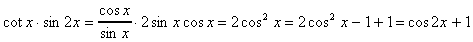
7. 
or 
So, in conclusion,
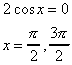
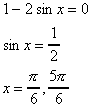
8. Multiply both sides by the common denominator, which "wipes
out" the denominator since the right side is 0. So x=3 is
the only solution. (Note that x=0 is not in the domain, but that
turns out to not be relevant to finding the solution.)
9. Factor out x and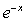 
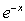
, and then set each
factor equal to zero. Since 
can't be
equal to zero for any value of x, the only solutions are 0 and
-3.
10. This is a quadratic-like equation. Solve by substitution,
letting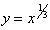 
. Then solve by factoring. Solve
for y first, then re-substitute to solve for x. The solutions
are 27 and -8.
11. You might not remember how to factor the sum of two cubics.
Can you remember that x+2 is a factor here, or that -2 is a solution
here? If so, then note that, to find the other factor besides
x+2, you can do polynomial long division. The other factor is
. Use the quadratic formula to find the
other two solutions. 
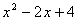
12. Factor out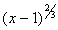 
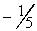
. Then reduce, so the numerator
is now simple. Multiply through by the common denominator, which
"wipes out" the denominator, so the only solution is
. Note that the left side isn't defined
when x=1, but it turns out that isn't relevant to the solution.
13. The method of elimination won't work here. (Do you see why?)
Using substitution, you solve the second equation for one of the
variables, probably for y. Then substitute y=1-3x into the first
equation and solve the resulting quadratic equation for x. That
results in two values for x; -2/5 and 1. Then you substitute each
of these into one of the equations for x and find the resulting
y. After that, you must check your solutions in the other equation.
Both work. 
14. This problem also involves simultaneous solution of two equations
in two variables and should be done by substitution. Since both
are already solved for y, it's easy. Just put in one of the equations'
expression for y into the other equation and solve for x. That
results in two values for x. Then you substitute each of these
into one of the equations for x to find the resulting y. After
that, you must check your solutions in the other equation. Both
work. 
15. You must use the exponential decay model. There are two (equivalent)
choices. One is to use the base e, and the other is to use the
base ½. I generally use the base e. So the model is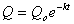 
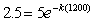
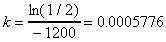
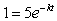
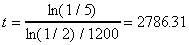
where t is the time. Now use the half-life in addition to all
the other given values to solve for k. Note that, at the end of
the time 1200, there will be half of the original amount left,
so the equation is 
. Use logarithms to
solve for k and get 
. Then use that k
and use the original amount is 5 and the final amount (Q) is 1.
. Using logarithms, as before, the solution
is 
years.
Last updated January 16, 1998. Send corrections or comments to
Mary Parker, mparker@austincc.edu