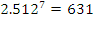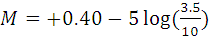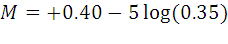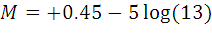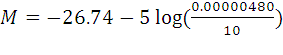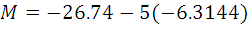|
Anyone who goes outside to see the night sky can tell that the stars are of different brightnesses. It would be nice to have a way to express a star’s brightness as a number, rather than just saying “that star’s pretty bright.” We have devices called photometers that can actually count the photons that come to us from the star, but those photons can number in the millions, numbers so large that they become useless. A system does exist for assigning a (fairly small and easy to remember) number to a star’s brightness, and it’s been around for quite awhile. About 2200 years ago, the Greek astronomer Hipparchos would take his students out under the stars, and rank them according to their brightness. The brightest stars were called “stars of the first magnitude,” the next brightest “stars of the second magnitude,” and so on, down to the faintest stars, which were “stars of the sixth magnitude.” The original system, therefore, was a very subjective system – that is, a matter of opinion. One person’s second magnitude star could be another’s third magnitude star, for example. In the modern era, we can assign a magnitude number to a photometer’s photon count total, making the system more objective with hard numbers. The first thing we notice about the magnitude system is that it is “backwards.” Brighter stars have lower numbers assigned to them. This is because the magnitude system is a ranking system. If you’re a college football team, you want a low number next to your name, preferably number one. Same thing with stellar magnitudes. In the modern system, you can even have negative magnitudes, for the very brightest objects like the Sun and the star Sirius. APPARENT
MAGNITUDE We were able to keep a lot of Hipparchos’
system intact. According to
photometer measurements, the faintest stars that can be seen with the
unassisted eye are around 100 times fainter than the brightest stars. In the original Hipparchan
system, there were 5 magnitudes of difference between these two types of star
(6-1). Therefore, the main
“rule” of the magnitude system is that a difference of 5 magnitudes corresponds to a factor of
100 times in brightness. If two
stars have magnitude values that differ by 5, the star with the lower magnitude
is 100 times brighter. So what if two
stars differ by one magnitude? We
may be tempted to say that one is twenty times brighter than the other, since
20 + 20 + 20 + 20 + 20 = 100.
However, that doesn’t work.
Magnitudes add together, but brightnesses multiply together. So we don’t need a number that adds together 5 times to make 100; we
need a number that multiplies
together 5 times to make 100.
This number is 2.5, or more accurately 2.512: 2.512 x 2.512 x 2.512 x
2.512 x 2.512 = approximately 100. So a second magnitude star is about two
and a half times brighter than a third magnitude star. A second magnitude star is not 5 times
brighter (2.5 + 2.5) than a fourth magnitude star, but rather 6.25 times
brighter (2.5 x 2.5). A second
magnitude star is 10 magnitudes different from a 12th magnitude
star; this means that the second magnitude star is 10,000 times brighter (100
x 100), not 200 times (100 + 100). To find how the
apparent brightness of two stars compare to each other, you can simply find
the difference in magnitudes, and raise the number 2.512 to that power, like
so:
9 – 2 = 7 and For another example, we can figure out how many times brighter the Sun is than the brightest star in the night sky, Sirius. Sirius has an apparent magnitude of -1.44 and the Sun has an apparent magnitude of a whopping -26.74. Find the difference and raise 2.512 to that power: -1.44 – 26.74 = 25.3 and ABSOLUTE
MAGNITUDE The original
system of magnitudes was developed to measure how bright a star appears to be
from Earth, what we now call apparent magnitude. But apparent magnitude is often a poor
indicator of how truly bright a star is.
For example, the stars of Orion’s Belt are some of the hottest,
most energetic stars in the Galaxy, and yet they are not among the “top
10” brightest stars in the sky.
The reason is that they are so far away. Sirius is the brightest star in the
sky, but not just because it is hot and luminous; it is also quite close to
us. Distance can make a luminous
star look dim and a dim star look deceptively bright. We can gauge a
star’s true energy output, called the luminosity, by calculating the
absolute magnitude. We remove the
effects of distance by mathematically “moving” the star to a
standard distance of 10 parsecs from Earth. So the absolute magnitude of a star is
the apparent magnitude it would have if it were at a distance of 10 parsecs
from us. If we know a
star’s distance in parsecs (D), and its apparent magnitude (m), we can
calculate the absolute magnitude (M) using the formula
The
“log” symbol is the logarithm function. For our purposes, it’s just a
button on your calculator.
Let’s do an example with a real star: Procyon in Canis Minor, which is 3.5 pc away, and has an apparent
magnitude of +0.40.
Do the stuff in parentheses first: Now take the logarithm of 0.35: Multiply the two negatives to get a positive: Now try it for the
famous star Betelgeuse, with a distance of 130 pc and an apparent magnitude
of +0.45, similar to Procyon:
Do the stuff in parentheses first: Now take the logarithm of 13: Note the logarithm was positive this time: Despite the fact
that they look almost identically bright to the eye, the two stars have
radically different luminosities!
Betelgeuse is the more luminous of the two, since its absolute
magnitude number is so small as to be negative. How many times more luminous is
Betelgeuse? We can use the same
technique as we did with apparent luminosity and apparent brightness: find
the difference in absolute magnitude, and raise the number 2.512 to that
power, like so:
2.70 – (-5.12) = +7.82 and If we do this
trick with the Sun, which is 0.0000048 parsecs (1 AU) from us, and has an
apparent magnitude of -26.74. We
can then find out what the Sun’s apparent magnitude would be if it were
10 parsecs away:
Do the stuff in parentheses first: Now take the logarithm of that small number: Note the logarithm was positive this time: And so if the Sun
were 10 parsecs from us, it would barely be visible to the naked eye. Earlier we saw that the Sun appears to
be 13 billion times brighter than Sirius in the sky. Sirius has an absolute magnitude of
+1.5, so it is actually more luminous than the Sun. We can find out how many times: +4.83 – (+1.5) = 3.33 and Try it yourself
for Procyon (about 7 times more luminous than the Sun) and Betelgeuse (about
9700 times!). Note that we can
turn the equation around, and find the apparent magnitude given the absolute
magnitude and distance. However,
we rarely need to do that, since we can measure the apparent magnitude
easily. ABSOLUTE
MAGNITUDE AND LUMINOSITY We saw above that if we know a star’s absolute magnitude is known, we can figure out how its luminosity compares to the Sun. We can turn that around, and figure out a star’s absolute magnitude if we somehow know its luminosity. The star’s luminosity (L) must be expressed in terms of the luminosity of the Sun; if you only know the luminosity in some other unit (Watts, perhaps), you must divide that number by the Sun’s luminosity in the same units. We can essentially turn the process above inside out, and use the formula
Note that the logarithm of 1 is zero, so if the star has the same luminosity as the Sun, it will have the same absolute magnitude, +4.83. Let’s do an example with the luminous star Arcturus, which is 110 times more luminous than the Sun:
Arcturus is rather luminous and fairly close, a combination which makes it the third brightest star in the sky. Now let’s look at Barnard’s Star, with a luminosity 0.00043 times that of the Sun:
It’s a good thing that Barnard’s Star is so close. If it were 10 parsecs away, it would be even fainter than it appears from Earth! You can use the data in the appendix for the brightest stars and the nearest stars to practice some more with these equations. |
 Updated 1/5/20 Updated 1/5/20Copyright Ó 2020 Austin Community College |