Calculus I:  Graphing and optimization review sheet

I suggest you alternate:  one graph, one application, one graph, one application...  That way, if you run out of time, you have done some of each.

For each of the following, find the critical points, inflection points, asymptotes, sign chart and graph:

f(x) = x^6 - 12000x^5 + 1000

Answer:

critical pts:  0, 10000
inflection pts:  0, 8000
asymptotes: zip
graph:  [Graphics:HTMLFiles/index_2.gif]

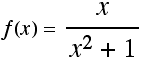
f(x) = x/(x^2 + 1)

Answer:

critical pts:  -1, 1
inflection pts:  0, -3^(1/2), 3^(1/2)
asymptotes:  hor: y = 0, vert: none
graph:  [Graphics:HTMLFiles/index_5.gif]

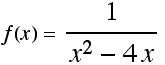
f(x) = 1/(x^2 - 4x)

Answer:

critical pts:   2 (undef: 0, 4)
inflection pts:  none
asymptotes:  hor: y = 0, vert: 0, 4
graph:  [Graphics:HTMLFiles/index_7.gif]

f(x) = x^2ln x

Answer:

critical pts:   e^(-1/2)
inflection pts:  e^(-3/2)
asymptotes:  hor: none, vert: none (not even at 0)
graph:  [Graphics:HTMLFiles/index_11.gif]

f(x) = 5x^(7/5) - 35x^(2/5)

Answer:

critical pts:   2 (undef at 0)
inflection pts: -3 (undef at 0)
asymptotes:  none
graph:  [Graphics:HTMLFiles/index_13.gif]

Solve the following:

If you need to print up posters with a total area of 154 inches^2, what dimensions should your poster be so that the printable area on it is as large as possible, if you want to have a 1 inch margin on the top and bottom and a 1.5 inch margin on the left and right sides?  (In other words, you want the space left over between the margins to be as large as possible.)

max:  Printed area
A = (l - 2) (w - 3)

However, the total area of the paper is 154, so:
l w = 154

Thus:
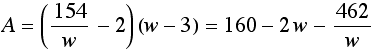
A = (154/w - 2) (w - 3) = 160 - 2w - 462/w

Domain:  0≤w

Solution:  approx. 15.20 inches wide × 10.13 inches tall

A car rental company has determined that if they charge $100 per car (per day), they will rent 150 cars.  For every $1 they raise the price, they will rent 5 fewer cars.  How much should they charge so they will earn the most money if they have 200 total cars they can rent?

max. Revenue:

R = (# of cars) (price per car)

If h = # of $1 price "increases",

R = (150 - 5h) (100 + h)

Domain:  -10≤h≤30  (Why?)

Solution:  charge $90 per car (per day)

Find the point on the graph of y^2 - x^2 = 1 that is closest to (2, 0) .

min:  distance
d = ((x - 2)^2 + (y - 0)^2)^(1/2)

However, the point (x, y) must lie on the given graph, so
y^2 - x^2 = 1

Thus:
d = ((x - 2)^2 + (x^2 + 1))^(1/2)

You could minimize this, but if you minimize the square of the distance (d^2), it will occur at the same x coordinate (why?) and will be lots easier:

D = (x - 2)^2 + (x^2 + 1)

Domain:  all real

Solution:  (1, 2^(1/2)) and (1, -2^(1/2))

A closed cylindrical can is to be made out of 120 inches^2 of aluminum.  What dimensions should this can have to hold the largest amount of liquid?

max:  volume
V = π r^2h

The total material (surface area) is:
120 = 2π r h + 2π r^2

Thus:
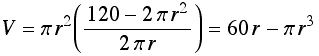
V = π r^2((120 - 2π r^2)/(2π r)) = 60r - π r^3

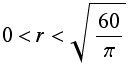
Domain:  0<r<60/π^(1/2)

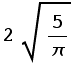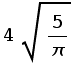Solution:  r = 2.52313 in. (2 5/π^(1/2)),  h = 5.04627 in. (4 5/π^(1/2))

Created by Mathematica  (November 17, 2004)