In[174]:=

Calculus II - Bonus Lab:
Taylor Series

Note:  In class I said this lab would consist of two parts (this was to be the second part), but I realized that the other part I was planning for you to use really wasn't workable for you, so this is it...

Taylor Series

To work with Taylor series in Mathematica, we first have to define the function we want to approximate and the "center" of the interval where we want to approximate it:

Now, if we want to work with finite Taylor polynomials, Mathematica has a built in function for that called Series.  There is a catch, however:  If you just type:

Mathematica gives you the Taylor series for expanded around c ( here) of degree 5.  However, notice the last term:    This means the "error" term is "on the order of" .  This is cool, but not very useful when you need to plug in a number:

Notice that the way to "plug in" is to use the notation.  However, notice that it still didn't give you an answer.  This is because of this extra "error term".  To make your series usable, you need to make it a "normal" polynomial:

Now, you can plug in :

Or graph it:

(Notice the Evaluate command we also had to add in; you must do this whenever you graph a Taylor series.)

Let's graph and the Taylor series together on the same graph:

If we want to generate a bunch of Taylor polynomials and graph them along with the original function, we can use the Table function:

The way this works is the term that sets k equal to 3 through 13, counting by 2 (so ), where is the degree of the Taylor series.  (I use the PlotRange command so that all the graphs show the same range on the Y axis, to make them easier to compare.  If you want hours of harmless amusement, double-click on one of these graphs and it will animate the whole set...)  If you would like to show all of these together on a single graph, you could use the Show command (remember, "fred" is the name we gave to this set of graphs):

Another graph that might be useful to look at is , where is the degree Taylor series  (you take the absolute value with Abs).:

If we want to examine how good an approximation the degree Taylor polynomial is on the interval , we could just look at the graph of the error on that interval:

We need the PlotRange→All command so Mathematica will show us everything (if you leave it out, Mathematica tries to be smart and figures there is a vertical asymptote there).  So, it looks like the degree Taylor polynomial is accurate to within about 0.005 on this interval.  What does our official error formula tell us?  It says, for a degree Taylor polynomial, the error should be less than: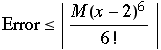

for this situation, where is the maximum value of the derivative on the given interval.  Now, we could possibly figure that out exactly (depending on how complicated is), but the details of that get a little too complicated for what I want to cover in this lab.  Let's just estimate it by looking at the graph of on the interval (and using the trace feature to estimate the maximum).  Remember, to take the derivative in Mathematica, you use the D command:  

So, it looks like .  Therefore, the error formula becomes:

So, on the entire interval, the largest error could occur at the endpoints:

Perhaps a more interesting thing to do is to graph the error formula over the desired interval:

Now, let's plot the actual error (red) and the Taylor error formula (yellow) on the same graph to compare:

So, since the Taylor error formula is so much larger than the true error, what is the point in even using it?  

Is it safe to use Taylor's error formula, since it is so "inaccurate"?

If you were to look at larger intervals, do you think this same pattern would hold (i.e., Taylor's error is much bigger than the true error)?  Check your guess by looking at and .  What happens on the interval ?  (Hint:  remember that will change on these intervals, when computing Taylor's error.  Show me the work and graphs for these intervals.)

If you were to use a higher degree Taylor polynomial, do you think the same pattern would hold as well (over the original interval )?  Check your guess by looking at and .  (When I was writing this problem, I originally wanted to ask you to look at , but this causes a very strange problem.  Look at this case and explain why you think the error behaves like it does.  Hint: it is very bizarre.)

Consider the function near :

Find the maximum error on the interval for a degree Taylor polynomial for this function.  

What is the maximum error for a degree Taylor polynomial for this function?  What is odd about this answer?

What is the maximum error for an degree Taylor polynomial for this function?  

Do you think these last two answers constitute a trend, or just a bizarre fluke?  Examine the maximum error of several higher order Taylor polynomials to help you decide.  (Show me your work here.)

Carefully examine graphs of and the Taylor polynomial for a , and a few of the higher order Taylor polyomials you found above to explain why the maximum errors seem surprising (at least for the degree polynomials).

What degree Taylor polyomial would you need to use to ensure that the maximum error on our interval was less than or equal to 0.01?

Created by Mathematica  (April 22, 2004)