In[49]:=

Calculus IV Lab 1: Limits and Functions

Limits

Taking a limit of a function of two variables can be very difficult.  Mathematica can take limits of a function of a single variable relatively easy:

However, it does not have a built-in command for finding the limit of a multi-variable function.  This is unfortunate (though not really surprising, considering the complications that can arise in 3 dimensions).  

For limits of functions of two variables, it can often be useful to graph the function around the limit point first.  This can give you an idea of whether the limit exists or not.  If it looks like it doesn't exist, the graph may give you some good ideas of what paths to test the limit along to look for differing values.  If you can find two different paths with two different limits, then you're done (the limit does not exist).  Mathematica can also aid you in taking limits along these paths.  If it looks like the limit does exist, you might be able to use Mathematica to ease your suffering as you try to prove it really does exist (sadly, Mathematica won't prove it for you...).

As an example, let's examine :

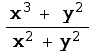In[90]:=

Out[90]=

It can also be very useful to look at a contour plot over the same region:

In[91]:=

Out[91]=

Although you can't really tell for certain here, it looks like the graph may approach different limits, depending upon what path you approach it on.  

Explain how the contour plot shows you the limit probably doesn't exist.

Now, let's test this on paths of the form y=m x:

In[92]:=

Out[92]=

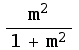
A fancier way to do this would be using the "ReplaceAll" operator:

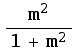
Since this depends upon m, the limit cannot exist.  On the other hand, consider :

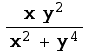In[93]:=

Out[93]=

In[94]:=

Out[94]=

The limit doesn't appear to exist here.  Again, let's check all linear paths through this point:

In[95]:=

Out[95]=

The contour lines here give you a clue:  they look (vaguely) parabolic.  So, let's try a parabolic path through the origin:

In[96]:=

Out[96]=

Of course, the contours actually look more like parabolas of the form x=m :

In[97]:=

Out[97]=

This goes to different limits for different values of m, so the original limit does not exist.  So, sometimes checking all lines isn't good enough.

Let's examine one more example:  

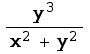
In[98]:=

Out[98]=

In[99]:=

Out[99]=

Here, it looks like the limit DOES exist.  Notice that this doesn't actually prove this; you still have to figure out a way to do that.  Mathematica may or may not help to do this.  Hint:  for (x,y) close to (0,0), 0≤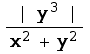≤|y|

For each of the following, use Mathematica to decide whether the limit exists or not.  Support your decision with appropriate graphs.  If it doesn't exist, confirm this fact algebraically.

1.  

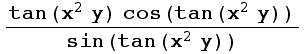
2.  

Note:  Mathematica uses the function Log for the natural logarithm (rather than ln).

3.  

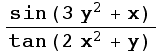
4.  

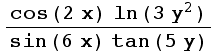
5.  

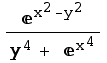
Functions

Composition of functions

There are different ways to define a function of more than one variable in Mathematica. For each of the following, give the dimension of the domain space and the dimension of the range space:

f[x_,y_,z_,t_]:=

g[x_,y_]:={y,}

h[t_]:={Sin[t],Cos[t],t,2t}

Taking the composition of two functions is relatively easy (don't forget to evaluate the functions above first):

However, try:

This doesn't work.  It SHOULD work (Why?), but it doesn't. To get around this problem, we will often define functions of more than one variable in the following way:

Now:

Will f[h[t]] work with the above definitions?  Should it?  If so, modify the definitions so it does.

Functions as arguments

Notice that if you have a function of a single variable, Mathematica knows what you mean by:

Partial derivatives are also pretty straightforward:

Sometimes, it is useful to define a function that operates on other functions.  So, for example, I could define a function to find the derivative matrix for functions from →:

(Notice that I needed to transpose the matrix to get the rows/columns to work out like we want.  I used MatrixForm just because it looks cool.)  However, you have to be really careful with these.  For example, if I just make one minor little change when calling it:

The problem is that, when we defined our function, we assumed that our variables would be called x and y, so any other choice of variables gets interpreted as a constant.  One way to fix this would be to explicitly specify your independent variables in the definition:

This now works, though at the cost of a bit of redundancy in calling the function.  (There are fancier tricks we could use to generalize this, but this is a good starting point.)

If you need to access one of the components of a vector, you can use the notation:

Define your own functions to compute the gradient (call it myGrad), divergence (call it myDiv), and curl (call it myCurl) of an arbitrary function of 3 variables.  (You may not use any of the built-in functions that handle these.)  Demonstrate that each of these actually work for a few different functions.

ParametricPlot3D with spherical and cylindrical coordinates

Mathematica has special built-in functions for graphing cylindrical and polar coordinates (CylinderPlot3D and SphericalPlot3D).  Unfortunately, these aren't really as versatile as we might wish.  For example, they wouldn't be capable of plotting something as simple as φ=.  Both of these commands are based on a much more flexible command, ParametricPlot3D.

ParametricPlot3D requires a function from either R→ or → as an input.  It will then graph the range of the function.  Thus:

In[88]:=

In[89]:=

Out[89]=

This error message is harmless.  If it annoys you, you can get rid of it by the following:

In[100]:=

Out[100]=

If you like, you can use ParametricPlot3D to draw a surface:

In[101]:=

In[102]:=

Out[102]=

You can even use ParametricPlot3D to graph a function of 2 variables:

In[103]:=

In[104]:=

Out[104]=

(If you had used the Plot3D function instead, it would have looked a little nicer...)

These two graphs look suspiciously alike.  Show that they are really the same surface.  Why do they look so different?

In order to use ParametricPlot3D to graph things in spherical and cylindrical coordinates, you must first develop a "change of variable" function. For example, a change of variable function for polar coordinates might look something like:

In[105]:=

In[106]:=

In[107]:=

Out[107]=

In[108]:=

Out[108]=

In[109]:=

Out[109]=

Warning:

In[110]:=

Out[110]=

What is wrong with this and why?

Fortunately, we are mainly interested in polarToRect (actually the equivalents for cylindrical and spherical coordinates).

Create 4 new functions: cylinderToRect (accepts points in the form {r,θ,z}), rectToCylinder, sphereToRect (accepts points in the form {ρ,θ,φ}), and rectToSphere to make the appropriate conversions.  Notice that all of these functions are from →.

You can use these new functions in conjunction with ParametricPlot3D to graph most equations in cylindrical and spherical coordinates. (You can even use it to graph cylindrical or spherical "parametric equations," something you don't see in many textbooks...)

For example, to graph something like ρ=Sin[θ]Cos[φ], you would do something like:

(Notice that you can only have 2 independent variables inside ParametricPlot3D, θ and φ in this case.)

Of course, the built-in SphericalPlot3D function could have done this (with less effort). However, you can also use your new functions to plot θ=:

Use the functions you developed above to graph the following (carefully choose what regions to graph over):

1. r=z cos(2θ)

2. r z sec(θ)=1

3. φ=ρ sin()

4. (θ)=

5. ρ=2t, θ=sin(5t), φ=cos(7t)

6. r=sin(u)cos(v), θ=sin(u v), z=cos(u+v)

Created by Mathematica  (January 26, 2005)