Deformations and Distortions
Sometimes, it makes sense to see what a function does to curves or surfaces from the domain space. So, for example:
![]()
![]()
This graphs these two lines in the domain space (the green one holds u constant and varies v, while the red one reverses this).
![domainCurves = ParametricPlot[{domainCurveU, domainCurveV}, {t, -5, 5}, PlotStyle {Red, Green}, AspectRatioAutomatic]](../HTMLFiles/index_162.gif)
![[Graphics:../HTMLFiles/index_163.gif]](../HTMLFiles/index_163.gif)
![]()
Our function transforms these two curves as follows:
![]()

![]()
![]()
![rangeCurves = ParametricPlot[Evaluate[{polarTransform[domainCurveU], polarTransform[domainCu ... ectRatioAutomatic, PlotStyle {Red, Green}, PlotRange {{-5, 5}, {-5, 5}}]](../HTMLFiles/index_169.gif)
![[Graphics:../HTMLFiles/index_170.gif]](../HTMLFiles/index_170.gif)
![]()
(With a little more work, you could construct a grid of these and see how it transforms in general.) Here's another example with a less common function:
![]()
![]()
![domainCurves = ParametricPlot[{domainCurveU, domainCurveV}, {t, -5, 5}, PlotStyle {Red, Green}, AspectRatioAutomatic]](../HTMLFiles/index_174.gif)
![[Graphics:../HTMLFiles/index_175.gif]](../HTMLFiles/index_175.gif)
![]()
![]()
![]()
![]()
![]()
![rangeCurves = ParametricPlot[Evaluate[{fTransform[domainCurveU], fTransform[domainCurveV]}], ... ectRatioAutomatic, PlotStyle {Red, Green}, PlotRange {{-5, 5}, {-5, 5}}]](../HTMLFiles/index_181.gif)
![[Graphics:../HTMLFiles/index_182.gif]](../HTMLFiles/index_182.gif)
![]()
Problem
Problems:
For each of the following functions, decide upon a suitable method to display the graph (using the techniques mentioned above or other appropriate methods) and use Mathematica to show it. Warning: The fanciest method is definitely not always the best choice. Choose ANY THREE of these to do.
1. T(x,y,t)=
T - The temperature (in °C) on the surface of a flat plate t hours after midnight at the point (x,y) (both measured in inches from the center).
2. L(x,y)=<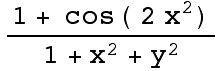 ,20
,20![]() (x y)>
(x y)>
L - The surface mass density (first coordinate of the range, in kg/![]() ) and temperature (second coordinate of the range, in °C) at a point (x,y) on a plane.
) and temperature (second coordinate of the range, in °C) at a point (x,y) on a plane.
3. ![]() ·polarTransform(u,v)
·polarTransform(u,v)
This is the same polarTransform function I defined in the explanatory text (above).
4. Cy(u,v,w)=<-u cos v,-u sin v,w>
Do this one twice. Once, consider that this gives the velocity vector field of a fluid. Now, consider it as a transformation (or "change of coordinates") and graph it.
5. D(u,v,t)=<u (cos v) (1+cos t),u (sin v)(1+ sin t)>
This is a change of coordinates that is time-dependent.
| Created by Mathematica (February 28, 2007) |