index_15.html

Graphing

You can also graph functions and parametric equations in these coordinate systems. In Lab 1, you wrote your own translation functions to do this for spherical and cylindrical coordinates. Let's look at another way this could be done, using the built-in Mathematica coordinate systems.

Let's graph ρ=Sin[θ]Cos[φ] (in spherical coordinates):

plotSurface = ParametricPlot3D[Evaluate[CoordinatesToCartesian[{ρ, ϕ, θ}, Spherical]], {ϕ, 0, π}, {θ, 0, 2π}, PlotPoints40]

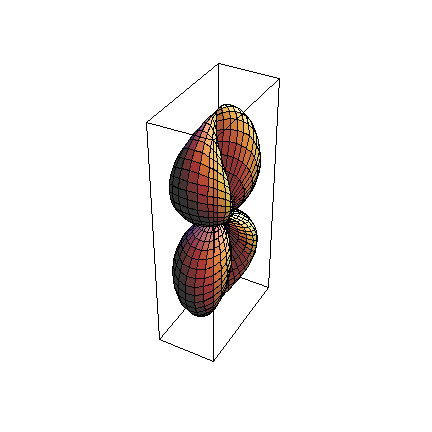
-Graphics3D-

To find the equation of a tangent plane to a surface at a point, remember that if you can express the equation as f[x,y,z]=0, you can find the equation of the tangent plane by setting ∇f[,,].{x-,y-,z-}=0. (The . stands for the dot product in Mathematica.)

So, for example, the above spherical equation could be written as:

$fSpherical[{ρ_, ϕ_, θ_}] := ρ - Sin[θ] Cos[ϕ]$

$General :: spell1 : Possible spelling error: new symbol name \"fSpherical\" is similar to existing symbol \"Spherical\". More…$

Converting this in Cartesian coordinates:

$fCartesian[{x_, y_, z_}] = fSpherical[CoordinatesFromCartesian[{x, y, z}, Spherical]]$

$General :: spell1 : Possible spelling error: new symbol name \"fCartesian\" is similar to existing symbol \"Cartesian\". More…$

(x^2 + y^2 + z^2)^(1/2) - (z Sin[ArcTan[x, y]])/(x^2 + y^2 + z^2)^(1/2)

So, to find the tangent plane at a point {,,} (in spherical coordinates), you first have to translate the point to Cartesian:

$ptCartesian = CoordinatesToCartesian[{3^(1/2)/2, π/6, π/2}, Spherical]$

${0, 3^(1/2)/4, 3/4}$

Find the gradient (again, in Cartesian):

$gradfCartesian[{x_, y_, z_}] = Grad[fCartesian[{x, y, z}], Cartesian]$

${x/(x^2 + y^2 + z^2)^(1/2) + (y z Cos[ArcTan[x, y]])/((x^2 + y^2) (x^2 + y^2 + z^2)^(1/2)) + ... ) + (z^2 Sin[ArcTan[x, y]])/(x^2 + y^2 + z^2)^(3/2) - Sin[ArcTan[x, y]]/(x^2 + y^2 + z^2)^(1/2)}$

It is very important that you use = above and not := or gradCartesian won't work correctly. This is a suble difference between = and :=

= evaluates the right hand side immediately, so it goes ahead and takes the gradient right away (before you plug in any values for x, y, and z.

:= doesn't evaluate the right hand side until later, so the gradient doesn't get computed until after you plug in for x, y, and z, which is a problem since we want to plug in numbers (to evaluate it at a point).

${0, 1, -2/3^(1/2) + 3^(1/2)}$

Now find the tangent plane:

tangentPlane = gradfCartesian[ptCartesian] . ({x, y, z} - ptCartesian)//N//FullSimplify

Let's graph this. There are a number of possibilities here. The easiest way is to use ContourPlot3D:

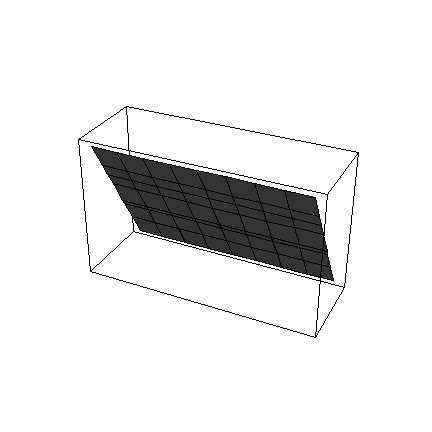
-Graphics3D-

So, if this worked, we should be able to display them together:

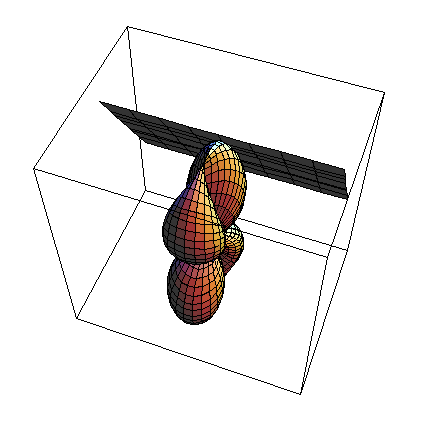
-Graphics3D-

Created by Mathematica (April 3, 2007)