Variation on a theme

Sometimes, your region of integration is a variant on something you are already familiar with.  For example, if you wanted to integrate:

Underscript[∫∫∫, D]x ^2y^4-z^2dV where D is the region between the graphs of:
    2x^2+4x+3y^2+z^2-3z=1 and 2x^2+4x+3y^2+z^2-3z=4
    
First, let's see what this actually looks like:

regionD = InequalityPlot3D[1≤ 2x^2 + 4x + 3y^2 + z^2 - 3z ≤4, {x}, {y}, {z}]

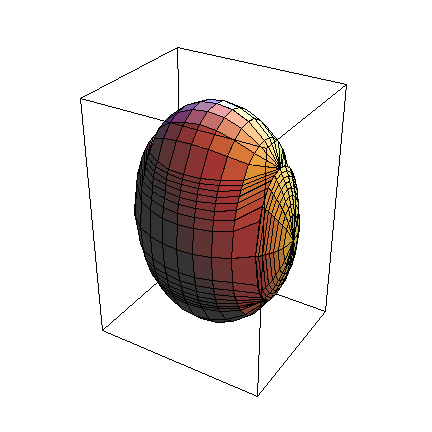
-Graphics3D-

⁃Graphics3D⁃

Well, it looks like an elllipsoid (or the region between two ellipsoids, actually, if you were to cut it open).  In fact, if you stare at the eqution a bit, this should become obvious to you.  We can complete the squares to find out what is going on:

2x^2+4x+3y^2+z^2-3z
=2(x^2+2x)+3y^2+(z^2-3z)
=2(x + 1)^2-2+3y^2+(z - 3/2)^2-9/4
So we get:
1≤2(x + 1)^2-2+3y^2+(z - 3/2)^2-9/4≤4
21/4≤2(x + 1)^2+3y^2+(z - 3/2)^2≤33/4

(There is probably a way to make Mathematica complete the squares for you, but unless I'm missing something, it's actually simpler just to do it by hand...)  So, what we have is a set of nested ellipsoids, centered at (-1,0,3/2).  A slightly different way to think of this is as spheres shifted from the origin to (-1,0,3/2) and stretched by a factor of (1/2)^(1/2)in the x direction and (1/3)^(1/2)in the y direction (why?).  

So, one thing we could do here is to take the standard coordinate transform for spherical coordinates and "distort" it in exactly this way.  So, if our standard spherical transform is:

mySphere[{ρ_, θ_, ϕ_}] := {ρ Cos[θ] Sin[ϕ], ρ Sin[θ] Sin[ϕ], ρ Cos[ϕ]}

Our distorted ellipsoidal form would be:

myEllipsoid[{ρ_, θ_, ϕ_}] := {ρ/2^(1/2) Cos[θ] Sin[ϕ] - 1, ρ/3^(1/2) Sin[θ] Sin[ϕ], ρ Cos[ϕ] + 3/2}

Notice that, in this case: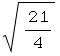

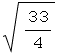21/4^(1/2)≤ρ≤33/4^(1/2), 0≤θ≤2π, 0≤φ≤π

(Why did I take the square root of the numbers for ρ?)  Let's graph this for the outer ellipse to check that we haven't done anything wrong here:

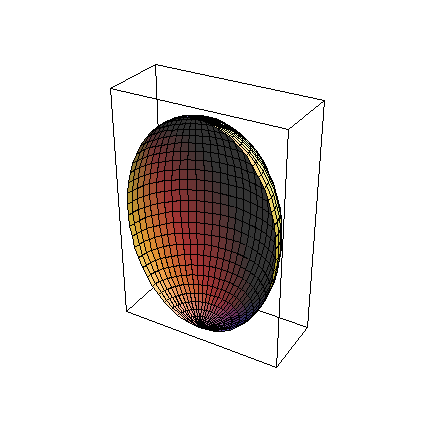
testRegion = ParametricPlot3D[myEllipsoid[{(33/4)^(1/2), θ, ϕ}], {θ, 0, π}, {ϕ, 0, π}]

-Graphics3D-

⁃Graphics3D⁃

Unfortunately, InequalityPlot3D can't handle trig functions, so I had to use ParametricPlot3D to draw the outer shell.  (Notice that I only used half the domain for θ.  This is so when I draw the two graphs together, I can see if they really coincide.)

Show[regionD, testRegion]

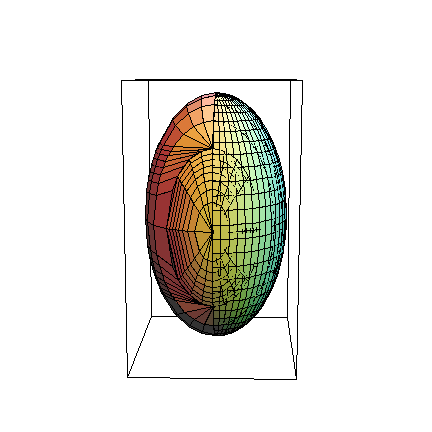
-Graphics3D-

⁃Graphics3D⁃

From here on out, it's just the usual stuff:

jDet = Det[D[myEllipsoid[{ρ, θ, ϕ}], {{ρ, θ, ϕ}}]]//FullSimplify

-(ρ^2 Sin[ϕ])/6^(1/2)

jDet = -jDet

(ρ^2 Sin[ϕ])/6^(1/2)

(This will now be positive everywhere in our domain...)

f[{x_, y_, z_}] := x ^2y^4 - z^2

∫_0^π∫_0^(2π) ∫_ (21/4)^(1/2)^(33/4)^(1/2) f[myEllipsoid[{ρ, θ, ϕ}]] jDetρθϕ

((13265 14^(1/2) - 20801 22^(1/2)) π)/2560

Created by Mathematica  (April 3, 2007) Valid XHTML 1.1!