In[31]:=

<<Graphics`

In[32]:=

<<RealTime3D`

In[33]:=

<<Calculus`

Calculus IV - Lab 3

Vector Integration

Work all of the following integrals entirely within Mathematica (i.e., even if you see a cool shortcut proving the integral equals zero, do it anyway). You may not work any of this by "cutting and pasting" results from one place to another.  You must set up your work so that, if I were to make a change to the definition of the function or the region, I could go through and re-execute everything and it would work with the new definitions (well, I might have to change some limits of integration as well).  Be sure to give a brief discussion of orientation where applicable.  Also, for each problem, tell me whether you can use Green's Theorem, Stokes' Theorem, Gauss' Theorem, or none of these on it.  Briefly explain why or why not and, if it is possible, do so and compare your results.  Use Mathematica to graph the objects you are integrating over as well.

Useful tip:  I just ran across the graphing functions InequalityPlot and InequalityPlot3D.  I had not found those before and they are really useful for graphing regions of integration (though they have some limitations, especially the 3D version).  You might find them useful...  Another function you might find useful is Reduce (it can simplify inequalities).  You will probably have to look these functions up on Wolfram's website (www.mathematica.com); they are in the help system for the version I am using, but I don't believe they were in the version 4 help system (though they do appear to work on version 4).  I include a few brief examples below; you will want to experiment with them a bit.  

InequalityPlot[1≤x^2 + 3y^2≤4, {x, -3, 3}, {y, -3, 3}]

[Graphics:HTMLFiles/index_5.gif]

⁃Graphics⁃

InequalityPlot[1≤x^2 + 3y^2≤4 && y≥x, {x, -3, 3}, {y, -3, 3}]

[Graphics:HTMLFiles/index_8.gif]

⁃Graphics⁃

InequalityPlot3D[x^2 + y^2 + z^2≤1&&x^2 + y^2≤z, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, PlotPoints30]

-Graphics3D-

⁃Graphics3D⁃

Reduce[x^2 + y^2≤1, Reals]

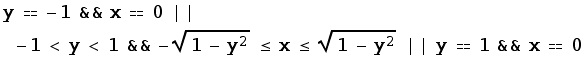
y -1&&x0 || -1<y<1&& -(1 - y^2)^(1/2) ≤x≤ (1 - y^2)^(1/2) || y1&&x0

(I'll leave it to you to think about how this might be useful...)

Problems:

∫_ ( Overscript[c, ⇀]) x^3(y^2 - z^2) s where Overscript[C, ⇀](t) = 〈cos t, cos 2t sin t, sin 2t sin t〉, 0≤t≤2π

∫_ ( Overscript[c, ⇀]) x^2x + y^3z e^x y + 4z^2 z where Overscript[C, ⇀] is composed of the line segments from (1, 2, 3) to (4, 5, 6) to (-6, 3, 1)

∫_ ( Overscript[c, ⇀])   Overscript[F, ⇀](x, y, z) · Overscript[s, ⇀] where Overscript[F, ⇀](x, y, z) = 〈y + z, -x^2, -4y^2〉 and Overscript[C, ⇀](t) is the boundary of the parallelogram through the points:  (0, 0, 0), (1, 2, 3), (-3, 6, 9), and (-4, 4, 6)

∫∫_S  x^2z ln y^2S where S is the surface of definted by y^2 = x^2 + z^2, 0≤y≤4.

∫∫_S curlOverscript[F, ⇀] · Overscript[S, ⇀] where Overscript[F, ⇀](x, y, z) = 〈x^5, -x^2y, x^5y^2z〉 and S is the portion of the cylinder x^2 + z^2 = 1 that is between the planes x + y + z = 0 and x + 2y + z = 2, oriented outwards.

∫∫_S Overscript[F, ⇀] · Overscript[S, ⇀] where Overscript[F, ⇀](x, y, z) = 〈x^2 + y, z sin x, y^3〉 and S is the surface z = x^2 + 2y^2 underneath the plane x + 2z = 1 (including the plane, so it is closed).

Created by Mathematica  (May 11, 2004)