Computation times (the cool part)
WARNING: If you want to actually run the examples below (as opposed to just looking at the numbers I give), you must make the definitions I ask for in the exercises above (maxMidPtError, maxSimpsonError, maxTrapError, etc.). If things don't work below, it is probably becuase you made a mistake on one or more of those or you forgot to execute them. You have been warned...
In order to get a better feel for how much effort it takes to use each of these methods, let's make some estimates about how long it actually takes to compute our definite integral to a desired degree of accuracy. If we want to make our approximation accurate to at least 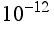 , for example, we can define:
, for example, we can define:
![RowBox[{maxErrorGoal, =, RowBox[{1., (10^(-12))}]}]](../HTMLFiles/index_69.gif)
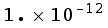
(Warning: We defined our definitions above to have a precision of 20 digits. If you want more accuracy than that, you will need to change those numbers in the definitions above.)
Using the left-hand (or right-hand) sum, we would need the following number of rectangles:
![subdivLR = Solve[maxLRError[n] maxErrorGoal]](../HTMLFiles/index_71.gif)
![RowBox[{{, RowBox[{{, RowBox[{n, , 1.18787*10^12}], }}], }}]](../HTMLFiles/index_72.gif)
Using Simpson's rule, on the other hand, we only need:
![subdivSimpson = Solve[maxSimpsonError[n] maxErrorGoal]](../HTMLFiles/index_73.gif)
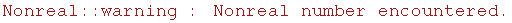
![RowBox[{{, RowBox[{RowBox[{{, RowBox[{n, , RowBox[{-, 911.809}]}], }}], ,, RowBox[{{, RowBox[{n, , 911.809}], }}], ,, {nNonreal}, ,, {nNonreal}}], }}]](../HTMLFiles/index_75.gif)
(Why do we get negative and complex solutions here?)
This is a huge difference. However, is this difference going to be noticeable to you if you have the computer do all the arithmetic for you? Let's do some very unscientific experimentation to find out. Mathematica has a function called Timing that allows you to time how much CPU time your computer needs to perform a calculation. What we are going to do is to sample this time for different numbers of subdivisions (10 through 10010 subdivisions, increasing by 1000 each time). Then, we will fit this data to a line so we can predict how long it would take this computer (the one you ran the test on) to compute one of these approximations for any arbitrary number of subdivisions. (Disclaimer: There are a lot of things that can affect this timing data, depending on what else the computer is doing while it is running. I make no claims about any real accuracy for this. However, it should be good enough to give us some idea of the relative effort involved in using these different approximations. That's good enough for me...)
Let's assume all these rules take about the same amount of time to compute the same number of subdivisions. (If you think about it, you will see that Simpson's rule isn't all that much more complicated than the left-hand rule to compute. There are slight differences, but it takes too long on my aging home computer to get good timing data for more than one test, so let's just get some timing data for the left-hand rule.)
![runTimeData = Table[{n, Timing[leftSum[n]][[1]]/Second}, {n, 10, 10010, 1000}]](../HTMLFiles/index_76.gif)
![RowBox[{{, RowBox[{RowBox[{{, RowBox[{10, ,, 0.01}], }}], ,, RowBox[{{, RowBox[{1010, ,, 1.072 ... ,, RowBox[{{, RowBox[{9010, ,, 9.935}], }}], ,, RowBox[{{, RowBox[{10010, ,, 10.995}], }}]}], }}]](../HTMLFiles/index_77.gif)
Now, we can fit this data to a line to develop a function that tells us approximately how long (in seconds) it would take to compute one of these rules for n subdivisions:
![timingFunction[n_] := Fit[runTimeData, {1, x}, x]/.xn](../HTMLFiles/index_78.gif)
If you are interested, it is:
![timingFunction[n]](../HTMLFiles/index_79.gif)
![RowBox[{RowBox[{-, 0.0117336}], +, RowBox[{0.00110064, , n}]}]](../HTMLFiles/index_80.gif)
Is it reasonable to fit this data to a line? This makes sense theoretically (think about it), and when we plot the timing data we obtained above along with our timingFunction, it at least looks reasonable.
![RowBox[{RowBox[{dataPlot, =, RowBox[{ListPlot, [, RowBox[{runTimeData, ,, RowBox[{PlotStyle, - ... }]}], ]}]}], ;, linearFit = Plot[timingFunction[x], {x, 0, 10000}], ;, Show[linearFit, dataPlot]}]](../HTMLFiles/index_81.gif)
![[Graphics:../HTMLFiles/index_82.gif]](../HTMLFiles/index_82.gif)
![[Graphics:../HTMLFiles/index_83.gif]](../HTMLFiles/index_83.gif)
![[Graphics:../HTMLFiles/index_84.gif]](../HTMLFiles/index_84.gif)
So, to compute our integral to the required degree of accuracy using the left-sum (or right-sum), it would take us:
![timingFunction[n] Second/.subdivLR](../HTMLFiles/index_86.gif)
![RowBox[{{, RowBox[{1.30742*10^9, , Second}], }}]](../HTMLFiles/index_87.gif)
Or, if that doesn't mean much to you, it would take:
![timingFunction[n]/60/60/24/365 Years/.subdivLR](../HTMLFiles/index_88.gif)
![RowBox[{{, RowBox[{41.4579, , Years}], }}]](../HTMLFiles/index_89.gif)
Simpson's rule, on the other hand, takes (ignore the negative and Nonreal answers):
![timingFunction[n] Second/.subdivSimpson](../HTMLFiles/index_90.gif)
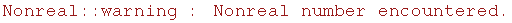
![RowBox[{{, RowBox[{RowBox[{RowBox[{-, 1.0153}], , Second}], ,, RowBox[{0.991836, , Second}], ,, Nonreal, ,, Nonreal}], }}]](../HTMLFiles/index_92.gif)
Pretty impressive, no? Now, let's take a look at time needed for computation as a function of the number of decimal places of accuracy you need (i.e., as a function of k, where 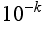 is your required error bound).
is your required error bound).
This defines functions to compute the time it takes to compute integrals to 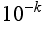 accuracy for each of our methods (these formulas are kind of complicated looking because I am having Mathematica only choose the positive answers; it isn't necessary for you to understand the details of these definitions in order to understand the results):
accuracy for each of our methods (these formulas are kind of complicated looking because I am having Mathematica only choose the positive answers; it isn't necessary for you to understand the details of these definitions in order to understand the results):
![timeLR[k_] := timingFunction[n]/. {n Select[n/.Solve[maxLRError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_95.gif)
![timeTrap[k_] := timingFunction[n]/. {n Select[n/.Solve[maxTrapError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_96.gif)
![timeMidPt[k_] := timingFunction[n]/. {n Select[n/.Solve[maxMidPtError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_97.gif)
![timeSimpson[k_] := timingFunction[n]/. {n Select[n/.Solve[maxSimpsonError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_98.gif)
Now let's look at a table of this information (you will probably need to scroll to the right to see the whole table). Note that all the time values are in seconds here.
![RowBox[{TableForm, [, RowBox[{RowBox[{Table, [, RowBox[{RowBox[{{, RowBox[{RowBox[{10., ^, (-k ... ", "Trapezoid rule", "Midpoint rule", "Simpson's rule"}}}], ]}]](../HTMLFiles/index_99.gif)
| Max error |
Left/right sum |
Trapezoid rule |
Midpoint rule |
Simpson's rule |
| 0.1 |
0.00134052 |
RowBox[{-, 0.00789932}] |
RowBox[{-, 0.00902237}] |
RowBox[{-, 0.00994901}] |
| 0.01 |
0.119008 |
0.000391535 |
RowBox[{-, 0.00315985}] |
RowBox[{-, 0.00856007}] |
| 0.001 |
1.29568 |
0.0266095 |
0.0153791 |
RowBox[{-, 0.00609015}] |
| 0.0001 |
13.0624 |
0.109518 |
0.0740043 |
RowBox[{-, 0.00169794}] |
| 0.00001 |
130.73 |
0.371698 |
0.259393 |
0.00611264 |
| 1.*10^-6 |
1307.4 |
1.20078 |
0.845645 |
0.020002 |
| 1.*10^-7 |
13074.1 |
3.82258 |
2.69954 |
0.0447012 |
| 1.*10^-8 |
130742. |
12.1134 |
8.56206 |
0.0886233 |
| 1.*10^-9 |
1.30742*10^6 |
38.3314 |
27.101 |
0.166729 |
| 1.*10^-10 |
1.30742*10^7 |
121.24 |
85.7262 |
0.305623 |
| 1.*10^-11 |
1.30742*10^8 |
383.42 |
271.115 |
0.552615 |
| 1.*10^-12 |
1.30742*10^9 |
1212.51 |
857.367 |
0.991836 |
| 1.*10^-13 |
1.30742*10^10 |
3834.3 |
2711.26 |
1.77289 |
| 1.*10^-14 |
1.30742*10^11 |
12125.2 |
8573.78 |
3.16183 |
| 1.*10^-15 |
1.30742*10^12 |
38343.1 |
27112.7 |
5.63175 |
| 1.*10^-16 |
1.30742*10^13 |
121252. |
85737.9 |
10.024 |
| 1.*10^-17 |
1.30742*10^14 |
383432. |
271127. |
17.8345 |
| 1.*10^-18 |
1.30742*10^15 |
1.21252*10^6 |
857379. |
31.7239 |
| 1.*10^-19 |
1.30742*10^16 |
3.83432*10^6 |
2.71127*10^6 |
56.4231 |
| 1.*10^-20 |
1.30742*10^17 |
1.21252*10^7 |
8.57379*10^6 |
100.345 |
How worried should you be about the negative times in the table above? What is causing those obviously anomalous results? (Or, I suppose it is possible that I have just invented time travel... I doubt it, but if I did, I want full credit and a cut of the profits...)
What conclusions can you draw about the relative effieiency of these different methods? Please try to say something a little more detailed than "Simpson's rule totally blows the others away"...
We could also plot the time necessary to compute the integral to within an accuracy of 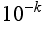 as a function of k (i.e., the number of decimal places, basically). In order to make all the graphs visible, I am only plotting times less than one hour (red is left-hand sum, green is trapezoid rule, blue is midpoint rule, and gold is Simpson's rule). Let's face it, if it takes more than an hour to compute, most of us will just give up and shut it down anyway.
as a function of k (i.e., the number of decimal places, basically). In order to make all the graphs visible, I am only plotting times less than one hour (red is left-hand sum, green is trapezoid rule, blue is midpoint rule, and gold is Simpson's rule). Let's face it, if it takes more than an hour to compute, most of us will just give up and shut it down anyway.
![RowBox[{Plot, [, RowBox[{{timeLR[k], timeTrap[k], timeMidPt[k], timeSimpson[k]}, ,, RowBox[{{, ... RowBox[{0, ,, RowBox[{60., *, 60}]}], }}]}], ,, PlotStyle {Red, Green, Blue, Gold}}], ]}]](../HTMLFiles/index_101.gif)
![[Graphics:../HTMLFiles/index_102.gif]](../HTMLFiles/index_102.gif)
What conclusions can you draw about the relative "efficiency" of the different methods?
What is the practical limit on the accuracy achievable via each method? (I arbitrarily decree one hour to be the longest time I am willing to wait on an answer. You could, of course, chose a longer or shorter time.)
How accurate could you make this integral using Simpson's rule if you allow it to run for an hour? Do you really believe this number? Why or why not?
Created by
Mathematica
(April 22, 2004)
![runTimeData = Table[{n, Timing[leftSum[n]][[1]]/Second}, {n, 10, 10010, 1000}]](../HTMLFiles/index_76.gif)
![RowBox[{{, RowBox[{RowBox[{{, RowBox[{10, ,, 0.01}], }}], ,, RowBox[{{, RowBox[{1010, ,, 1.072 ... ,, RowBox[{{, RowBox[{9010, ,, 9.935}], }}], ,, RowBox[{{, RowBox[{10010, ,, 10.995}], }}]}], }}]](../HTMLFiles/index_77.gif)
![RowBox[{RowBox[{dataPlot, =, RowBox[{ListPlot, [, RowBox[{runTimeData, ,, RowBox[{PlotStyle, - ... }]}], ]}]}], ;, linearFit = Plot[timingFunction[x], {x, 0, 10000}], ;, Show[linearFit, dataPlot]}]](../HTMLFiles/index_81.gif)
![[Graphics:../HTMLFiles/index_82.gif]](../HTMLFiles/index_82.gif)
![[Graphics:../HTMLFiles/index_83.gif]](../HTMLFiles/index_83.gif)
![[Graphics:../HTMLFiles/index_84.gif]](../HTMLFiles/index_84.gif)
![timeLR[k_] := timingFunction[n]/. {n Select[n/.Solve[maxLRError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_95.gif)
![timeTrap[k_] := timingFunction[n]/. {n Select[n/.Solve[maxTrapError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_96.gif)
![timeMidPt[k_] := timingFunction[n]/. {n Select[n/.Solve[maxMidPtError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_97.gif)
![timeSimpson[k_] := timingFunction[n]/. {n Select[n/.Solve[maxSimpsonError[n] 10^(-k)], #>0&][[1]]}](../HTMLFiles/index_98.gif)
![RowBox[{TableForm, [, RowBox[{RowBox[{Table, [, RowBox[{RowBox[{{, RowBox[{RowBox[{10., ^, (-k ... ", "Trapezoid rule", "Midpoint rule", "Simpson's rule"}}}], ]}]](../HTMLFiles/index_99.gif)
![RowBox[{Plot, [, RowBox[{{timeLR[k], timeTrap[k], timeMidPt[k], timeSimpson[k]}, ,, RowBox[{{, ... RowBox[{0, ,, RowBox[{60., *, 60}]}], }}]}], ,, PlotStyle {Red, Green, Blue, Gold}}], ]}]](../HTMLFiles/index_101.gif)
![[Graphics:../HTMLFiles/index_102.gif]](../HTMLFiles/index_102.gif)